引言
前两个月学习DGIM算法的时候,实现了一下。最近整理代码时发现还有些问题,于是重新写一份,顺带将相关内容整理成blog。
在许多数据挖掘场景中,在分析挖掘的时候我们通常都已掌握了所需的全部数据集。数据流(Data Stream)跟数据集(Dataset)所不同的是,数据流是非静态的,它的分布随时间而变化,它可以是无限长度的,有些场景下数据流入速度十分快。一般来说,对于数据流的处理有如下两种方式
-
对数据流进行采样
-
通过滑动窗口进行处理
假如我们要计算比特流最近的N位中有多少为1的位,N(滑动窗口的大小)非常大,我们无法存储这最近的N位数据,在这种情况下我们是无法得知准确的答案的。但是,对于一个差不多的答案,我们是可以接受的。DGIM算法可以给我们一个近似的答案,对于一个数据流只需使用O(log N)的空间,结果误差不超过50%。
DGIM算法
DGIM算法的主要思想是用bucket来记录数据流中的1的个数,它保存一个范围内1的个数(记作size以方便说明)以及该范围的结束位的时间戳,它记录的1的个数必须是2的指数大小。
对于任意某一个size,系统运行时的某一时刻都只会存在要么1个要么2个该size的bucket,如果有3个size的bucket,则将其中时间戳最早的两个bucket合并为大小为两倍size的bucket。这里可以联系2048小游戏的规则来理解一下。
所有的bucket的时间戳都不会重叠。bucket按照size排序,所以时间戳早的bucket的size大小是不小于时间戳比较晚的bucket的size。
当一个新的比特位进来之后,那些超出滑动窗口大小的bucket需要删除掉。
下图是一个例子,其中将数据流表示成几个bucket(2个size为1的,1个size为2的,2个size为4的和1个size为8的)。
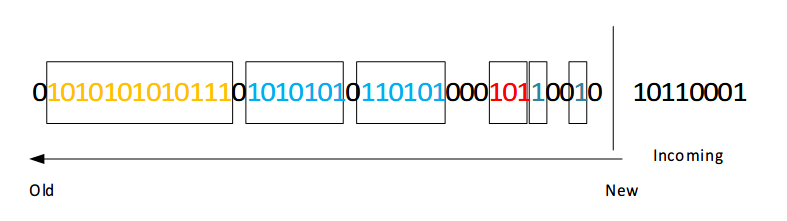
当进来一个位1之后,bucket表示更新如下图所示。
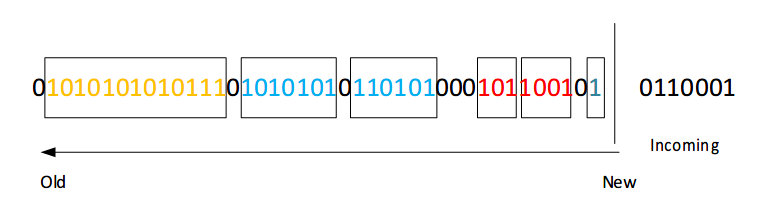
更新规则
当一个比特位进来的时候,更新时间戳。通常可以将(索引编号 mod N)来作为时间戳,这里mod表示取余,N为滑动窗口的大小。然后把那些时间戳已经超出滑动窗口的bucket丢弃掉。
如果当前位为0,无需动作。
如果当前位为1,则
-
创建一个size为1的bucket,设置其时间戳。
-
如果已有三个size为1的bucket,则将其中最早的两个bucket合并为一个size为2的bucket,将这两个bucket中出现比较晚的的时间戳作为新bucket的时间戳。
-
如果已有三个size为2的bucket,则将其中最早的两个bucket合并为一个size为4的bucket,如此更新下去。
查询结果
将滑动窗口中所有的bucket的size加起来,然后减去最早的那个bucket的一半size。
换一种说法,就是除了最早的那个bucket,将其他所有的bucket的size加起来,然后再加上0.5 × 最早那个bucket的size。
因为我们不清楚最早的那个bucket中有多少个1是还留在滑动窗口中,在没有其他信息的情况下只能假设其中0和1均匀分布了。
特点
-
方法比较简单
-
空间复杂度低
-
误差率有限制,不大于50%
误差率的证明
假设最早的那个bucket(记作b_e)的size为 。
因为在查询结果时我们加上了b_e的一半size,当b_e只有结束位位于滑动窗口中时,此时会造成最大的误差,大小为。对于每个size,滑动窗口中都至少存在一个bucket,所以滑动窗口中1的真正个数不小于 。所以误差率最多为 , 约等于50%。
Python实现
主要用了一个字典,key为bucket的size,value为对应size的bucket列表。
这里并没有定义bucket对象,直接用bucket的时间戳表示一个bucket了。
import math
filename = "test.txt"
container = {}
windowsize = 1000
timestamp = 0
updateinterval = 1000# no larger than the windowsize
updateindex = 0
keysnum = int(math.log(windowsize, 2)) + 1
keylist = list()
# initialize the container
for i in range(keysnum):
key = int(math.pow(2, i))
keylist.append(key)
container[key] = list()
def UpdateContainer(inputdict, klist, numkeys):
for key in klist:
if len(inputdict[key]) > 2:
inputdict[key].pop(0)
tstamp = inputdict[key].pop(0)
if key != klist[-1]:
inputdict[key * 2].append(tstamp)
else:
break
def OutputResult(inputdict, klist, wsize):
cnt = 0
firststamp = 0
for key in klist:
if len(inputdict[key]) > 0:
firststamp = inputdict[key][0]
for tstamp in inputdict[key]:
print "size of bucket: %d, timestamp: %d" % (key, tstamp)
for key in klist:
for tstamp in inputdict[key]:
if tstamp != firststamp:
cnt += key
else:
cnt += 0.5 * key
print "Estimated number of ones in the last %d bits: %d" % (wsize, cnt)
with open(filename, 'r') as sfile:
while True:
char = sfile.read(1)
if not char:# no more input
OutputResult(container, keylist, windowsize)
break
timestamp = (timestamp + 1) % windowsize
for k in container.iterkeys():
for itemstamp in container[k]:
if itemstamp == timestamp:# remove record which is out of the window
container[k].remove(itemstamp)
if char == "1":# add it to the container
container[1].append(timestamp)
UpdateContainer(container, keylist, keysnum)
updateindex = (updateindex + 1) % updateinterval
if updateindex == 0:
OutputResult(container, keylist, windowsize)
print "\n"