聚类
聚类是一种非监督式的机器学习方法。对于监督式的分类问题,其 learning dataset 中的每一个样本点都有对应的标签,其目标为学习一个模型使得其对未知数据的预测表现最好。而对于非监督式的聚类问题,其数据集中并没有提供标签,而且它不像分类问题那样有明显的 训练-预测 过程。
所谓聚类,即是将一堆的数据点划分到一定数量的簇(cluster)中,使得位于同一个簇中的数据点之间的相似度高(距离小),位于不同簇中的数据点之间的相似度低(距离大)。
聚类可以帮助我们发现数据的结构。它有着很多的应用:比如社交网络的社群检测,搜索结果的组织等。常用的聚类方法有:层次聚类,K-Means聚类,谱聚类等。
K-Means 算法
K-Means 是一个非常简单、经典的聚类算法。K-Means 的优化目标为最小化各数据点到其所属中心点的距离的平方的和,表达式如下:
直接求解该优化问题是NP-Hard的,可以采用迭代的方法:先固定,得到最优的分配(将数据点分配给离它最近的那个 centroid 所代表的簇中,这样即可得到当前 RSS 的最小值);然后在当前数据点分配的情况下得到最优的 centroids 。在每一次迭代中都最小化了目标函数,这使得 K-Means 能够保证得到一个局部最优解。虽然不能保证得到全局最优解,但通常情况下得到的局部最优解也足够好了。
算法流程
基本的 K-Means 聚类算法流程如下:
-
选取 K 个数据点作为初始的 centroids
-
将所有数据点分配到离其最近的那个 centroid 所表示的簇中
-
更新每个簇的 centroid 为该簇中所有数据点的均值
-
重复第2、3步直至 centroids 不再改变或者超出给定的迭代次数
复杂度分析
假设数据集中有 n 个数据点,K-Means 聚类需要 l 次迭代,假设每个数据点的维度为 m , k 为簇的数量。由于计算两个数据点之间的距离的复杂度为 O(m) ,则第2步的复杂度为 O(knm) 。第3步中,每个数据点都要对某个 centroid 做一个加法的动作,复杂度为 O(nm) 。所以总的复杂度为 O(lknm) 。
Python 实现
生成数据
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib
%matplotlib inline
mean1 = (0, 8)
mean2 = (5, 5)
mean3 = (1, -1)
cov = [[1, 0], [0, 1]]
x1 = np.random.multivariate_normal(mean1, cov, 20)# shape: 20*2
x2 = np.random.multivariate_normal(mean2, cov, 30)
x3 = np.random.multivariate_normal(mean3, cov, 20)
x = np.concatenate((x1, x2, x3), axis=0)
print x.shape生成的用例数据如下图,不同颜色标识不同的数据来源。
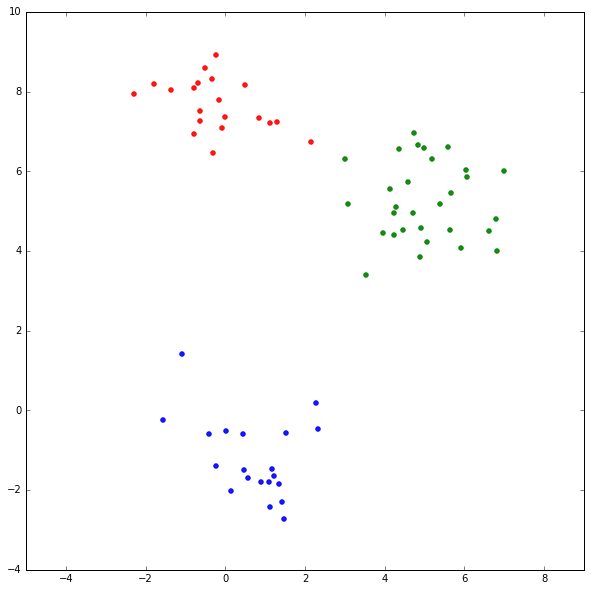
K-Means 实现
下面的实现是用类来组织的,其实更好的方法是使用嵌套函数,这里就不改进了。
class kmeansclustering:
def __init__(self, data, k=2, maxiter=100, epsilon=1e-12):
'''
data: input data, numpy ndarray
k: the number of centroids
'''
self.data = data
self.k = k
self.maxiter = maxiter
self.epsilon = epsilon
self.N = len(data)
self.colors = cm.rainbow(np.linspace(0, 1, self.k))
self.classes = np.zeros(self.N, dtype=int)
def getdistmat(self):
data_sqrowsum = np.sum(self.data * self.data, axis=1)
cen_sqrowsum = np.sum(self.centroids * self.centroids, axis=1)
return np.outer(data_sqrowsum, np.ones((1, self.k))) - 2 * np.dot(self.data, self.centroids.T) \
+ np.outer(np.ones((self.N, 1)), cen_sqrowsum)
def compute_obj(self):
tempsum = 0
for i in xrange(self.N):
tempsum += np.sum(np.square(self.data[i] - self.centroids[self.classes[i]]))
return tempsum
def kmeans(self, plot=False):
numiter = 0
# initialize centroids
self.centroids = self.data[np.random.choice(self.N, self.k, replace=False), :]
if plot:
self.draw(False)
preval = self.compute_obj()
while numiter < self.maxiter:
distmat = self.getdistmat()
# assign datapoints to clusters
self.classes = np.argmin(distmat, axis=1)
# update centroids
for c in xrange(self.k):
self.centroids[c] = np.mean(self.data[self.classes == c], axis=0)
objval = self.compute_obj()
# check convergence
if preval - objval < self.epsilon:
print 'exit before max iterations'
break
preval = objval
if plot:
self.draw(True)
numiter += 1
def draw(self, plotcen=True):
'''
only for 2-dimension cases
'''
plt.figure(figsize=(10,10), facecolor='white')
colors_data = [self.colors[c] for c in self.classes]
plt.scatter(self.data[:, 0], self.data[:, 1], color=colors_data, marker='.', alpha=0.9, s=80)
plt.axis('equal')
if plotcen:
plt.scatter(self.centroids[:, 0], self.centroids[:, 1], marker='o', color=self.colors, s=120)
plt.show()上面的距离用的是欧氏距离,可以根据需要改成其他的距离。
getdistmat 方法采用向量化计算,输入参数为 data (大小为 n × m) 和 centroids (大小为 k × m),返回的是一个 n × k 的矩阵。每一行为一个大小为 k 的向量,其中的元素表示该数据点到 k 个 centroid 的欧式距离的平方。由于开方运算开销较大,而且我们关注的是某个点到各个 centroid 距离的相对大小关系,故这里没有进行开方运算。
下面以一个二维的例子说明一下。 表示第一个数据点到第一个 centroid 的距离的平方。 表示第一个数据点的第一个维度的值, 表示第一个 centroid 的第一个维度,其余同理。
\[ {d_{11}} = {({x_{11}} - {c_{11}})^2} + {({x_{12}} - {c_{12}})^2} \]
将上式中的平方项展开,即
\[ {d_{11}} = {x_{11}}^2 + {x_{12}}^2 + {c_{11}}^2 + {c_{12}}^2 - 2{x_{11}}{c_{11}} - 2{x_{12}}{c_{12}} \]
可以看到,结果分为三项:
-
该数据点各个维度的平方的和
-
某个 centroid 的各个维度的平方的和
-
该数据点与 centroid 的内积。
针对这三项分别构造矩阵。
-
先求得各数据点各维度的平方的和,为一个大小为 n 的向量,让其跟一个大小为 k 的向量 做外积即可得到一个 n × k 的矩阵。
-
求各 centroid 各维度的平方的和,为一个大小为 k 的向量,让一个大小为 n 的向量 跟其做外积即可得到一个 n × k 的矩阵。
-
第3项为 -2 倍的内积, 即 -2 × data · centroids (大小为 n × k)。
将上面三个矩阵加起来即可得到距离矩阵。
运行例子一
kmc = kmeansclustering(x, 3)第一次迭代结果(大的点表示 centroid ):
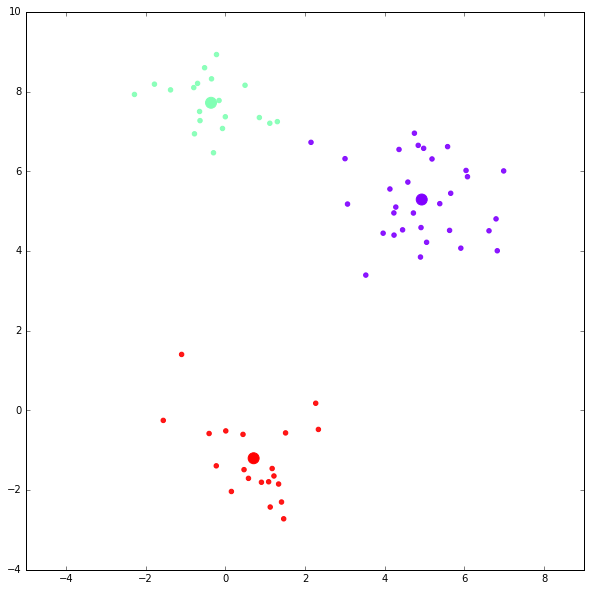
第二次迭代结果:
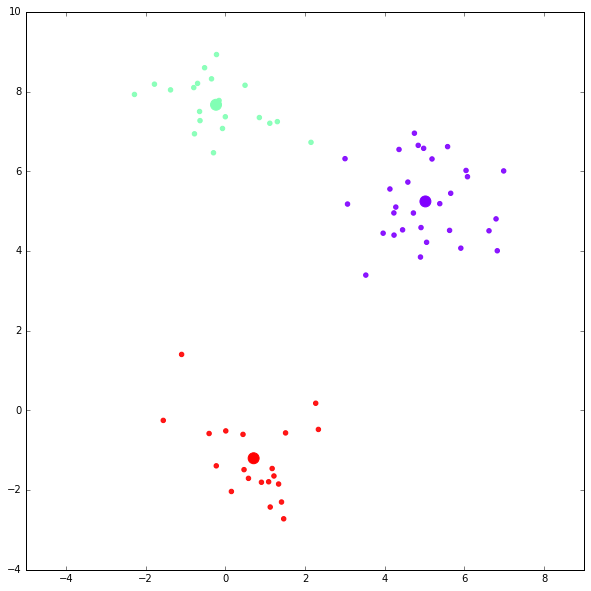
迭代完成。
运行例子二
对同样的数据再做一次 K-Means 聚类。
kmc = kmeansclustering(x, 3)第一次迭代结果:
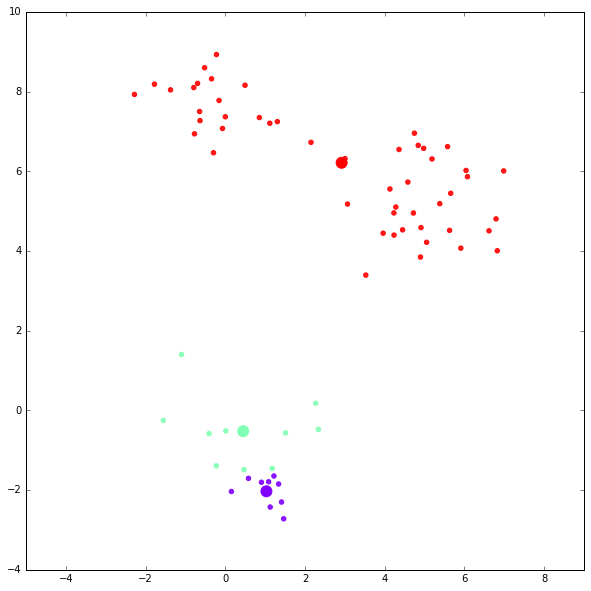
第二次迭代结果:
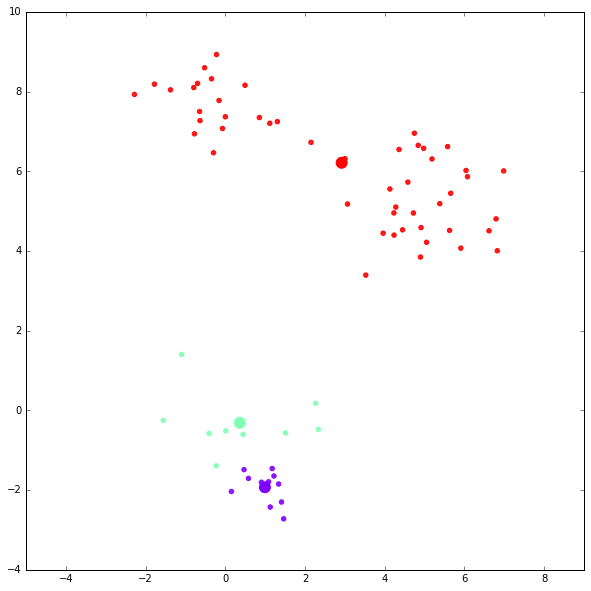
第三次迭代结果:
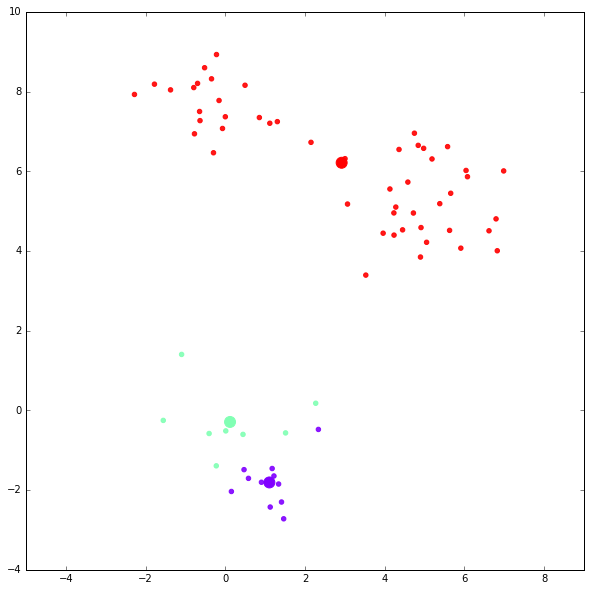
第四次迭代结果:
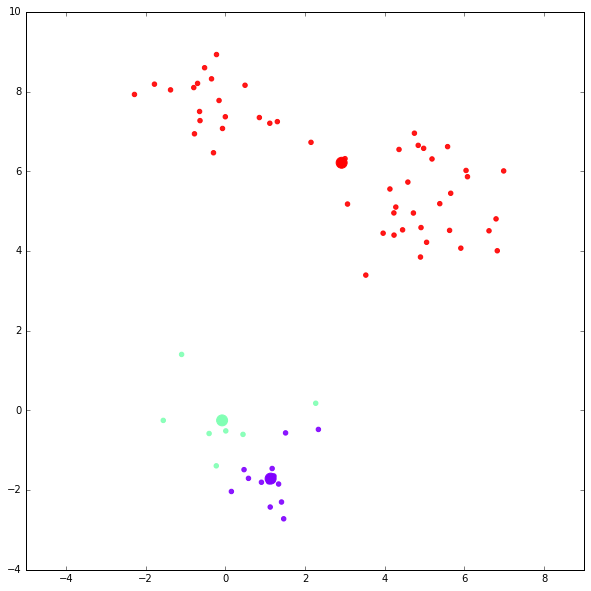
第五次迭代结果:
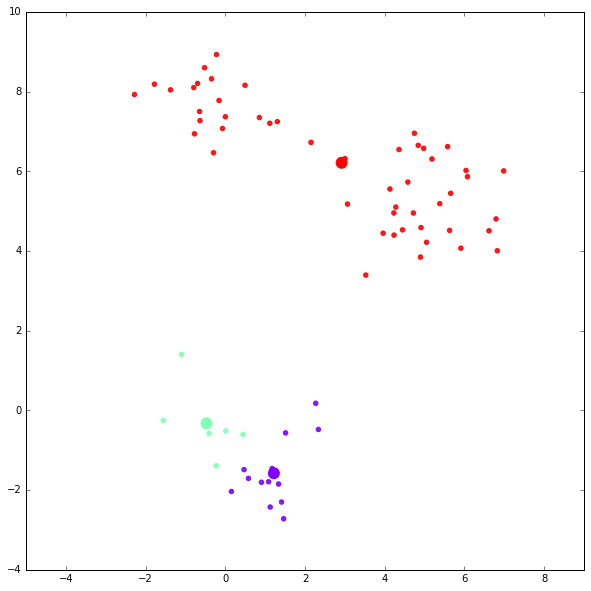
迭代完成。
可以看到,这次聚类的结果比较不理想,K-Means 受 centroid 的初始化影响很大。
K-Means 特点
优点:
-
比较简单,实现容易
-
复杂度较低,速度快
-
通常效果还不错
缺点:
-
需要给定簇的个数
-
对异常值比较敏感
-
结果受初始的 centroids 影响,是局部最优而非全局最优
-
对非凸形状的簇效果较差
K-Means 杂谈
由于 K-Means 的结果受初始的 centroids 影响,通常我们可以多次运行,从而得到一个比较满意的结果。可能的改进思路有
-
根据 global mean 随机扰动来生成初始 centroids
-
使用启发式方法来初始化 centroids
-
使用别的聚类方法(比如层次聚类)的结果来初始化 centroids
由于 K-Means 需要指定簇的数量,也就是 K 的值,通常的做法是为不同的 K 值做 K-Means 聚类,然后根据某个聚类评估指标来选取最优的聚类结果。
K-Means 作为一个简单的、经典聚类算法,可作为别的算法中的某个 routine ,比如可以用在自上而下的层次聚类中作为分割一个 cluster 的 routine。K-Means 有很多的变种,比如 buckshot 算法,比如半监督式聚类中的 COP K-Means 等,这里就不再展开了。