离散随机数生成、数组shuffle排列

前言：由于之前算法学习学得比较散，基础有些弱，所以买了本算法书，是普林斯顿大学的教授Robert Sedgewick写的《算法》第四版，打算细致地学习一下，并在博客中记录一下自己的学习和思考过程。错误以及偏颇之处敬请指正。

离散随机数生成

代码分析

书中根据离散概率随机返回int值（出现i的概率为a[i]）的代码如下

public static int discrete(double[] a)
{// a[]中各元素之和必须等于1
	// StdRandom是作者写的库，random方法返回均匀分布在0到1之间的随机数
	double r = StdRandom.random();
	double sum = 0.0;
	for (int i = 0; i < a.length; i++)
	{
		sum = sum + a[i];
		if(sum >= r) return i;
	}
	return -1;
}

乍一开始，没看明白为什么这样就能根据数组a中的概率来生成随机数，后来通过一个例子来想了想。

假设一个随机变量X，它的取值有{0,1,2,3}，它们对应的概率为{0.3,0.1,0.2,0.4}，则X的分布如下图所示。

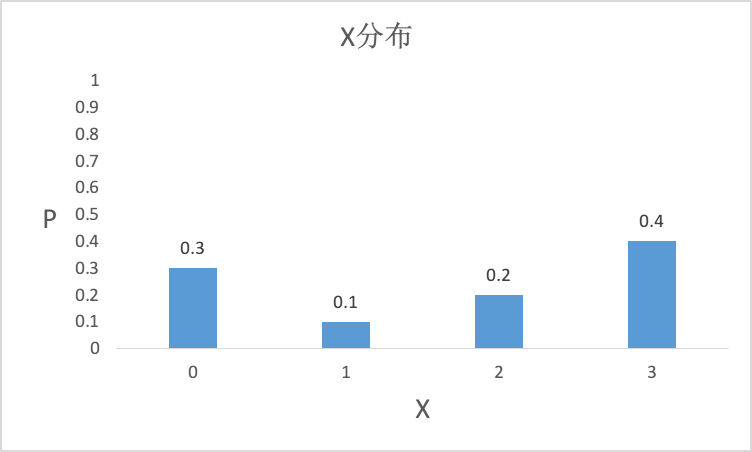
X的CDF如下图所示。

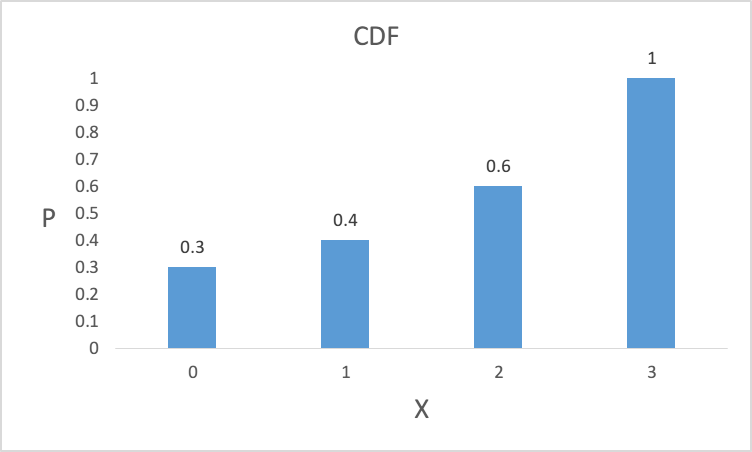
从上图可以看出，纵轴上的取值可以分为四个区间，分别为[0,0.3], (0.3,0.4], (0.4,0.6], (0.6,1.0]，区间长度表明了该区间对应X取值的出现概率。选择一个均匀分布在[0, 1]范围内的随机数，它必然会落在上面四个区间中的一个，返回该区间对应的X的取值，这样即可按照随机变量X的分布来产生随机数。

更多关于生成特定分布随机数的内容参考 传送门

代码改进

直接计算出CDF的数组，避免计算部分的重复。

注：下面的代码实现只是用于说明想法，不是最好的实现方式。

public static double[] cdf;

public static int discrete(double[] a)
{// a[]中各元素之和必须等于1
	// StdRandom是作者写的库，random方法返回均匀分布在0到1之间的随机数
	double r = StdRandom.random();
	if (cdf == null)
	{
		cdf = new double[a.length];
		for (int i = 0; i < a.length; i++)
		{
			if (i == 0)
				cdf[i] = a[i];
			else
				cdf[i] = cdf[i-1] + a[i];
		}
	}
	for(int i = 0; i < cdf.length; i++)
	{
		if(cdf[i] >= r) return i;
	}
	return -1;
}

数组shuffle排列

代码分析及证明

书中用于数组shuffle的代码如下：

public static void shuffle(double[] a)
{
	int N = a.length;
	for (int i = 0; i < N; i++)
	{// 将a[i]和a[i..N-1]中任意一个元素交换
		// uniform(k)方法返回均匀分布在0到k之间的随机整数，不包含k
		int r = i + StdRandom.uniform(N - i);
		double temp = a[i];
		a[i] = a[r];
		a[r] = temp;
	}
}

一开始的时候，由于对问题的formulation不对，跟踪分析的是整个过程中原来第 I 个元素可能的交换过程，把问题复杂化了。试图通过一个小的例子来找出规律，弄了比较长时间，结果也是不对。可见合理的 problem formulation 是多么的重要！！！

长度为N的数组，假设数组元素不重复，那么一共会有N!种可能的排列方式，一个合理的shuffle方法应该使得这N!种排列都是等可能的。

首先，我们考虑一个元素（称为A）的可能位置。先对其余N-1个元素进行shuffle，这N-1个元素有(N-1)!种。对于一个N-1个元素的排列，它有N个位置可供A插入，从而形成N个元素的一种排列。这样看来，元素A在某个特定位置时有(N-1)!种排列，那么元素A在该位置的概率应该为$\frac{ {\left( {N - 1} \right)!} } { {N!} } = \frac{1}{N}$，也就是说元素A在排列的任意位置的概率都是一样的。

换句话说，如果某个元素在长度为N的排列的每个位置的概率都是一样的的话，那么该shuffle方法是合理的。

下面来证明一下为什么上面的乱序实现（选择从i到N-1之间的随机整数）是合理的。

根据位置来分析，对于位置F，它的值经过F次选择交换之后就可以被确定了。

F=1时，N个元素中选一个，即每个元素最终在位置1的概率为$\frac{1}{N}$。

F=2时，对于任意一个元素，如果它最终在位置2，则必须满足第一次没被选中，第二次被选中，则概率为$\frac{ {N - 1} }{N} \times \frac{1}{ {N - 1} } = \frac{1}{N}$ 。

…

F=i 时，对于任意一个元素，它最终在位置i的概率为$\frac{ {N - 1} }{N} \times \frac{ {N - 2} }{ {N - 1} } \times ... \times \frac{ {N - i} }{ {N - i + 1} } \times \frac{1}{ {N - i} } = \frac{1}{N}$

由上可知每个元素在任意位置的概率都为1/N，说明上面的shuffle（打乱）的方法是合理的。

糟糕的打乱

下面是一种糟糕的打乱方法：乱序代码中选择的是一个从0到N-1而非i到N-1之间的随机整数，代码如下：

public static void shuffleTerrible(double[] a)
{
	int N = a.length;
	for (int i = 0; i < N; i++)
	{// 将a[i]和a[0..N-1]中任意一个元素交换
		// uniform(k)方法返回均匀分布在0到k之间的随机整数，不包含k
		int r = StdRandom.uniform(N);
		double temp = a[i];
		a[i] = a[r];
		a[r] = temp;
	}
}

这种做法，对于位置F上的元素，需要在N次选择交换之后才能确定。根据上面的观点（每个元素在任意位置的概率都为1/N，则该shuffle方法是合理的），只需验证每个数在任意位置的概率不等于1/N即可。

事实上，对于任意一个元素，它始终留在原位的概率为 ${p_0} = {\left( {\frac{ {N - 1} }{N} } \right)^N}$，将${p_0}$的值跟$\frac{1}{N}$进行比较，可得$N \times \ln \left( {N - 1} \right) = \left( {N - 1} \right) \times \ln \left( N \right)$，它的唯一实数解约等于3.29，如下图所示。

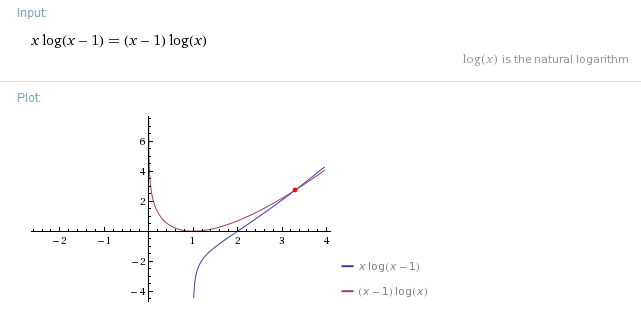
当N大于等于4时，${p_0}$的值大于$\frac{1}{N}$。而该元素最终保持在原来的位置的概率是大于${p_0}$的，因为中间过程它可能被交换到别的位置然后又交换回来。从而，任意一个元素最终留在原来位置的概率不等于$\frac{1}{N}$，这种打乱方法是糟糕的。